Question

Explain how to solve 2^x + 1 = 9 using the change of base formula log base b of y equals log y over log b. Include the solution for x in your answer. Round your answer to the nearest thousandth. (10 points)

Answer 1

x = 3.000

Explanation:

You want the solution to 2^x +1 = 9 using the change of base formula.

Solution

To use any sort of logarithms in the solution process, you need to get the exponential term by itself. We do this by subtracting 1 from both sides.

2^x +1 = 9 . . . . . . given

2^x = 8 . . . . . . . . subtract 1

This is turned into a linear equation by taking the logarithm of both sides. You can get there directly using base-2 logarithms, or you can use logs of any base with the change of base formula:

log₂(2^x) = log₂(8)

x = log₂(8) = ln(8)/ln(2) = 3

The value of x is 3 (exactly).

__

Additional comment

The change of base formula is ...

`\log_b(x)=(\log(x))/(\log(b))`

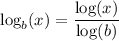
where the logs on the right are to any base, as long as it is the same for both.

If you recognize 2^3 = 8, you can match exponents of 2^x = 2^3 to get x=3. Effectively this is taking logarithms to base 2 without ever writing "log( )".

<95141404393>