Question

Anthony is going to invest in an account paying an interest rate of 3.7% compounded daily. How much would Anthony need to invest, to the nearest dollar, for the value of the account to reach $13,700 in 12 years?

Answer 1

Anthony would need to invest approximately $9,181.84 to the nearest dollar for the value of the account to reach $13,700 in 12 years with a 3.7% interest rate compounded daily.

To find out how much Anthony needs to invest today for the value of the account to reach $13,700 in 12 years with an interest rate of 3.7% compounded daily, you can use the compound interest formula:

`A = P(1 + r/n)^{(nt)`

Where:

A = the future value of the investment ($13,700 in this case)

P = the initial principal (the amount Anthony needs to invest)

r = the annual interest rate (3.7% or 0.037 as a decimal)

n = the number of times interest is compounded per year (daily, so n = 365)

t = the number of years (12 years in this case)

We want to solve for P. Let's plug in the values:

13,700 =
`P(1 + 0.037/365)^{(365*12)`

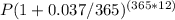
Now, let's calculate the exponent part first:

1 + 0.037/365 = 1.00010136986 (rounded to 10 decimal places)

Now, raise this to the power of (365 * 12):

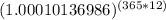`(1.00010136986)^{(365*12)` ≈ 1.49411962

Now, the equation becomes:

13,700 = P * 1.49411962

To solve for P, divide both sides of the equation by 1.49411962:

P = 13,700 / 1.49411962 ≈ 9,181.84

So, The answer is $9,181.84.

Answer 2

Antony needs to invest approximately $8,788 for the value of the account to reach $13,700 in 12 years.

The formula for the compound interest is expressed as:

`A = P( 1 + (r)/(n))^(nt)`

Where A is the accrued amount, P is the principal, r is the interest rate and t is time.

Given that:

Accrued amount A = $13,700

Interest rate r = 3.7% = 3.7/100 = 0.037

Time t = 12 years

Compounded daily n = 365

Principal P =?

Now, plug these values into the above formula and solve for principal P:

`A = P( 1 + (r)/(n))^(nt)\\\\P = (A)/(( 1 + (r)/(n))^(nt) ) \\\\P = (13700)/(( 1 + (0.037)/(365))^(365*12) ) \\\\P = (13700)/((1 + 0.0001013698630137)^(4380)) \\\\P = (13700)/(1.0001013698630137^(4380)) \\\\P = \$ 8,788`

Therefore, the money that needs to be invested is approximately $8,788.