If
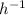 is the inverse of h , option B
is the inverse of h , option B
 is the value of
is the value of
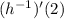 .
.
To find the value of
 , we can use the fact that the derivative of an inverse function is the reciprocal of the derivative of the original function at the corresponding point.
, we can use the fact that the derivative of an inverse function is the reciprocal of the derivative of the original function at the corresponding point.
Let's denote the inverse function
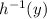 , where y is the output value of h(x). So,
, where y is the output value of h(x). So,
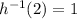 since h(1)=2.
since h(1)=2.
Now, the derivative of h(x) is given by
 . We can evaluate
. We can evaluate
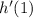 to find the slope of the tangent line to h(x) at x=1:
to find the slope of the tangent line to h(x) at x=1:
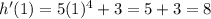
Now,
 is the reciprocal of
is the reciprocal of
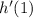 :
:
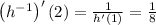
So, the correct answer is (B)

Complete Question:
The function h is given by
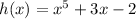 and
and
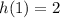 . If
. If
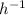 is the inverse of h, what is the value of
is the inverse of h, what is the value of
 ?
?
a.
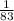
b.

c.

d. 1
e. 8