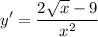Question

Find the derivative of the function.

Answer 1

`\displaystyle y'= (2√(x) - 9)/(x^2)`

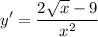
Explanation:

We will use the quotient rule, the power rule, and exponent rules to find the derivative of the given function.

The derivate rule for differentiation states:

`\displaystyle \text{If}\;\;\;y=(u)/(v) \;\;\text{then}\;\; (dy)/(dx) =(v(du)/(dx) -u(dv)/(dx) )/(v^2)`

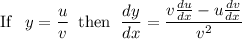
In other words, if you have two terms being divided by each other, multiply the denominator by the derivative of the numerator, subtract the numerator being multiplied by the derivative of the denominator, and divide this all by the denominator squared (Low-d-high minus high-d-low all over low squared, as my math teacher said.).

Given:

`\displaystyle y=(9+7x-4√(x) )/(x)`

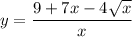
The square root of x is equal to x raised to the one-half:

`\displaystyle y=(9+7x-4(x^(1)/(2) ) )/(x)`

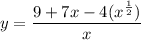
Quotient rule:

`\displaystyle y'= (x(7-2x^(-1)/(2) )- (9+7x-4(x^(1)/(2) )(1))/((x)^2)`

Multiply and simplify the fraction:

`\displaystyle y'= ((7x-2x^(1)/(2) )- (9+7x-4(x^(1)/(2) ))/(x^2)`

`\displaystyle y'= (7x-2x^(1)/(2) - 9-7x+4x^(1)/(2))/(x^2)`

`\displaystyle y'= (2x^(1)/(2) - 9)/(x^2)`

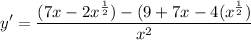
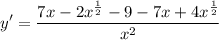
X raised to the one-half is equal to the square root of x:

`\displaystyle y'= (2√(x) - 9)/(x^2)`