Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

`x=39^o,\ y=7^o`

Explanation:

`\mathrm{Solution:}\\(3x)^o=117^o\ \ \ \ \mathrm{[Opposite\ angles\ of\ rhombus\ are\ equal.]}\\\mathrm{or,\ }x^o=39^o\\\\(9y)^o+117^o=180^o\ \ \ \ \mathrm{[Being\ cointerior\ angles.]}\\\mathrm{or,\ }(9y)^o=63^o\\\mathrm{\therefore\ }y=7^0`

Answer 2

1st picture:

• x=39
• y =7

2nd picture:

• x =90°
• y=62°

3rd picture:

• x= 36°

Explanation:

For 1st Picture:

(3x)°=117° Opposite angle of the rhombus are equal.

dividing both side by 3, we get

`\tt x=(117)/(3)`

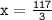
x=39

and

(9y)°+117°=180° Being co interior angle

9y=180-117

9y=63

y=63/9

y=7

Therefore, x=39 and y =7.
`\hrulefill`

For 2nd picture:

See the attachment:

x°=90° since the diagonals of a rhombus bisect each other perpendicularly.

again,

m∡CDE= 28° since the diagonals of a rhombus bisect each vertex angle.

again

m∡CDE + m∡ DAE=m∡ CEA

Exterior angle is equal to the sum of two opposite interior angle of a triangle.

substituting value

28°+y°=90°

y=90-28

y=62°

Therefore, x =90° and y=62°

`\hrulefill`

for 3rd question:

Since it is a equilateral triangle, it's all interior angle equal be equal and it is 60°.

so,

m∡MNL = 60°

again,

m∡MNL + m∡MNo=180° being linear pair

60°+ 3x+12=180°

3x+72=180

3x=180-72

3x=108

x=108/3

x=36

therefore, x= 36°