Question

The plane through the points (4, 1, 4), (5, −8, 6), and (−4, −5, 1)

Answer 1

The equation of the plane passing through the points (4, 1, 4), (5, −8, 6), and (−4, −5, 1) is (3x - 2y + z = 11).

Step-by-step explanation:

To find the equation of the plane, we can use the general form of the equation for a plane: Ax + By + Cz = D), where (A, B, C) is the normal vector to the plane. To determine the normal vector, we can find two vectors lying on the plane, calculate their cross product, and normalize the result.

Let P1(4, 1, 4), P2(5, −8, 6), and P3(−4, −5, 1) be the given points. Two vectors on the plane can be obtained as
`v 1​ ​ =P 2​ −P 1​ and �2⃗=�3−�1v 2​ ​ =P 3​ −P 1`.

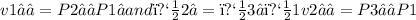The normal vector can be found by taking the cross product:
`N` =
`N = v 1​ ​ × v 2​ ​ .`

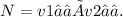
After obtaining the normal vector, we normalize it to ensure it represents a unit vector. The coefficients A, B, C of the plane's equation are then taken as the components of the normalized normal vector, and D is found by substituting any of the given points into the equation Ax + By + Cz = D.

In this case, after the calculations, we find the equation of the plane to be 3x - 2y + z = 11, where A = 3, B = -2, C = 1, and D = 11.