Question

A satellite weighing 5,400 kg is launched into orbit 3.6400 x 107 m above the center of the earth.

The mass of Earth is 6.0 × 1024 kg. The gravitational constant is 6.673 × 10–11 N•m2/kg2.

The gravitational force of Earth on the satellite is ___



Group of answer choices

9.1 x 10^4

1.6 x 10^3

2.1 x 10^6

Answer 1

`\tt F=1.63*10^3 N`

Step-by-step explanation:

Gravitational force is defined as the force of attraction between two objects with mass. It is a fundamental force of nature, and it is what keeps us on the ground and what keeps the planets in orbit around the Sun.

The gravitational force between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers

For the Question:

We can use the following formula to calculate the gravitational force between the Earth and the satellite:

`\boxed{\tt F =( G * M * m )/( r^2)}`

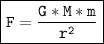
Where:

F is the gravitational force

G is the gravitational constant
`\tt (6.673 * 10^(-11) Nm^2/kg^2)`

M is the mass of the Earth
`\tt (6.0 * 10^24 kg)`

m is the mass of the satellite
`\tt (5,400 kg)`

r is the distance between the satellite and the center of the Earth
`\tt (3.6400 * 10^7 m)`

Plugging in these values, we get the following:

`\tt F = (6.673 * 10^(-11) * 6.0 * 10^(24)* 5,400 )/( (3.6400 * 10^7 )^2)`

`\tt F=1.63*10^3 N`

Therefore, answer is
`\tt F=1.63*10^3 N`