Answer:
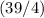 .
.
Step-by-step explanation:
In the vector notation in this question, the coefficient of
 is the
is the
 -component of the vector while the coefficient of
-component of the vector while the coefficient of
 is the
is the
 -component.
-component.
For example, in this question, the
 -component of acceleration would be
-component of acceleration would be
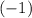 , while the
, while the
 -component of this acceleration would be
-component of this acceleration would be
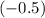 .
.
Because the the
 -component of acceleration is negative, the velocity of this particle would keep decreasing.
-component of acceleration is negative, the velocity of this particle would keep decreasing.
While the
 -component of the velocity of the particle was initially
-component of the velocity of the particle was initially
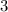 (which is positive,) this value would become zero and then negative after some amount of time. When that happens, the direction of the motion of this particle in the
(which is positive,) this value would become zero and then negative after some amount of time. When that happens, the direction of the motion of this particle in the
 -component would be reversed, and the particle would not go any further in its original direction of motion.
-component would be reversed, and the particle would not go any further in its original direction of motion.
Divide the change in velocity
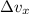 in the
in the
 -component by the
-component by the
 -component of acceleration
-component of acceleration
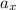 to find the time required for the particle to reach the maximum
to find the time required for the particle to reach the maximum
 -coordinate:
-coordinate:
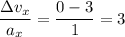 .
.
In other words, the
 -coordinate of this particle would be maximized exactly at
-coordinate of this particle would be maximized exactly at
 units of time.
units of time.
Given that the acceleration of this particle is constant, apply the following SUVAT equation to find the position
 of this particle at time
of this particle at time
 :
:
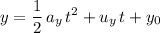 ,
,
Where:
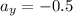 is the acceleration of this particle in the
is the acceleration of this particle in the
 -component,
-component,
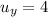 is the initial velocity of this particle in the
is the initial velocity of this particle in the
 -component, and
-component, and
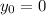 is the
is the
 -coordinate of the initial position (the origin) of this particle.
-coordinate of the initial position (the origin) of this particle.
Evaluate this expression at
 when the
when the
 -coordinate of this particle is maximized:
-coordinate of this particle is maximized:
 .
.
In other words, when the
 -coordinate of this particle is maximized, the
-coordinate of this particle is maximized, the
 -coordinate of this particle would be
-coordinate of this particle would be
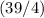 .
.