Question: 1.
The interval notation [a,b] denotes a closed interval, which means that the endpoints a and b are included in the interval. In this case, the interval is defined as all real numbers x such that a ≤ x ≤ b.
So the answer is b) [a,b]

Question: 2.
The square root function is undefined when the radicand (the expression under the square root) is negative.
Therefore, the domain of the function
 is all real numbers x such that
is all real numbers x such that
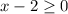 , or
, or
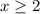
So the answer is d. x≥2

Question: 3.
One root is is 5. This means that if we substitute 5 for x, the equation will be equal to zero.
If we substitute 5 for x, we get:

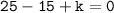
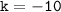
Therefore, the value of k is d. 10.

Question: 4.
The expression
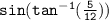 can be simplified using the following steps:
can be simplified using the following steps:
Use the trigonometric identity that relates the sine and tangent functions:
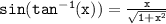
In this case,
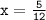 . Substituting it into the identity, we have:
. Substituting it into the identity, we have:
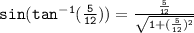
Find the square of
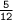 and the square root of the sum:
and the square root of the sum:
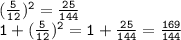
Substitute these values back into the expression:
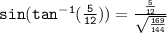
Rationalize the denominator:

Therefore,
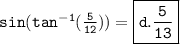

Question: 5
An angle bisector is a line that divides an angle into two congruent angles. The angle bisectors of two intersecting lines are always perpendicular to each other.
Since there are two angles between two intersecting lines, there are 2 angle bisectors.
Ans: b. 2

Question: 6
Two vectors are collinear if they lie on the same line. If
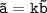 , then
, then
 and
and
 are scalar multiples of each other, which means that they lie on the same line.
are scalar multiples of each other, which means that they lie on the same line.
Therefore,
 and
and
 are b. collinear vectors.
are b. collinear vectors.

Question: 7
Since A and B are independent events, we know that:
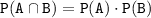
Substituting the given values, we have:
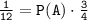
Solving for P(A), we get:
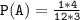
Therefore,
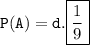

Question 8.
We can evaluate the limit
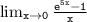 , by using
, by using
L' Hospital rule.
Taking the derivative of the numerator and denominator with respect to x. we have:
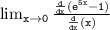
Applying the derivative, we get:
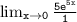
Now, we can substitute x = 0 into the expression:
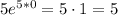
Therefore, the limit
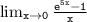 is equal to d. 5.
is equal to d. 5.

Question 9.
If
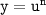 , where u is a function of x and n is a constant, we can find
, where u is a function of x and n is a constant, we can find
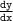 using the chain rule.
using the chain rule.

In this case,
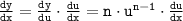
Therefore,
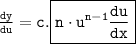

Question. 10
In order to evaluate can apply the power rule of integration and the constant multiple rule.
Integrating term by term, we get:
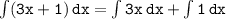
Applying the power rule of integration, we have:
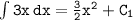
Integrating the constant term, we have:
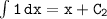
Putting everything together, we have:
![\int\limits_0^2 (3x+1) \, dx = \left[(3)/(2)x^2 + x\right]_0^2](https://img.qammunity.org/2024/formulas/mathematics/high-school/2wbs03fhmtjhdober6vou8l2zormmg4c6m.png)
Now, we substitute the limits of integration:
![\tt \left[(3)/(2)(2)^2 + 2\right] - \left[(3)/(2)(0)^2 + 0\right]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ynfar64p77si4psp04tw3d1xycamsljpdx.png)
Simplifying:
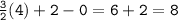
Therefore,
 = c. 8
= c. 8

Question 11.
Step-by-step explanation:
The rule works by dividing the interval of integration into a number of subintervals, and then approximating the integral as the sum of the trapezoids formed by the subintervals.
The number of subintervals is denoted by n. As n increases, the approximation of the integral becomes more accurate.
so ans is d. n equal sub-intervals