Question

Variables x and y are connected by the equation y = x / tanx. Given that x is increasing at the rate of 2 units per second, find the rate of increase of y when x is π/4

​

Answer 1

(2 - π) units per second.

Explanation:

Connected rates of change are when two or more variables are related, and the rates of change of these variables are connected or dependent on each other. This means that the change in one variable affects the change in another variable.

To find the rate of change of y (with respect to time, t), we need to find the equation for dy/dt. To do this, find dy/dx and dx/dt, and multiply them together.

To find dy/dx, differentiate y with respect to x using the quotient rule.

`\boxed{\begin{minipage}{5.5 cm}\underline{Quotient Rule for Differentiation}\\\\If $y=(u)/(v)$ then:\\\\\\$\frac{\text{d}y}{\text{d}x}=\frac{v \frac{\text{d}u}{\text{d}x}-u\frac{\text{d}v}{\text{d}x}}{v^2}$\\\end{minipage}}`

`\textsf{Given:} \quad y=(x)/(\tan x)`

`\textsf{Let}\;u=x \implies \frac{\text{d}u}{\text{d}x}=1`

`\textsf{Let}\;v=\tan x \implies \frac{\text{d}v}{\text{d}x}=\sec^2x`

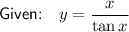
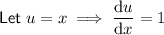
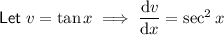
Therefore:

`\frac{\text{d}y}{\text{d}x}=(\tan x \cdot 1 - x \cdot \sec^2x)/(\tan^2x)`

`\frac{\text{d}y}{\text{d}x}=(\tan x - x \sec^2x)/(\tan^2x)`

`\frac{\text{d}y}{\text{d}x}=(\tan x)/(\tan^2x) - (x \sec^2x)/(\tan^2x)`

`\frac{\text{d}y}{\text{d}x}=(1)/(\tan x) - (x )/(\sin^2x)`

`\frac{\text{d}y}{\text{d}x}=\cot x- x \csc^2x`

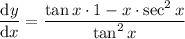
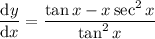
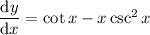
Given x is increasing at the rate of 2 units per second:

`\frac{\text{d}x}{\text{d}t}=2`

Now we have dy/dx and dx/dt, we can multiply them to get dy/dt:

`\frac{\text{d}y}{\text{d}t}=\frac{\text{d}y}{\text{d}x} * \frac{\text{d}x}{\text{d}t}`

`\frac{\text{d}y}{\text{d}t}=(\cot x- x \csc^2x) * 2`

`\frac{\text{d}y}{\text{d}t}=2\cot x- 2x \csc^2x`

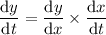
To find the rate of increase of y when x is π/4, substitute x = π/4 into dy/dt:

`\frac{\text{d}y}{\text{d}t}=2\cot \left((\pi)/(4)\right)- 2\left((\pi)/(4)\right) \left(\csc\left((\pi)/(4)\right)\right)^2`

`\frac{\text{d}y}{\text{d}t}=2(1)- \left((\pi)/(2)\right) \left(√(2)\right)^2`

`\frac{\text{d}y}{\text{d}t}=2- \left((\pi)/(2)\right) \left(2\right)`

`\frac{\text{d}y}{\text{d}t}=2- \pi`

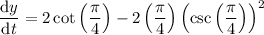
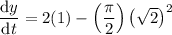
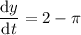
Therefore, the rate of increase of y when x is π/4 is (2 - π) units per second.