Answer:
1. c) x = 45
2. 3 < x < 27
3. d) 4.5
Explanation:
The interior angles of a triangle sum to 180°.
Therefore, equate the sum of the given expressions of angles A, B and C to 180°, and solve for x.
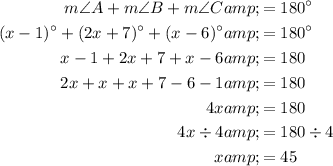
Therefore, the value of x is x = 45.

According to the Triangle Inequality Theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Given two sides are 12 cm and 15 cm in length, and the third side is "x", we can create three inequalities:
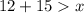

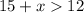
Solving the inequalities gives:
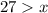


Combining the solutions we get:

Therefore, the range of possible lengths for the third side of the triangle is 3 < x < 27.

According to the Triangle Inequality Theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Given two sides lengths are 26 and 30, and the third side is "x", we can create three inequalities:

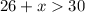
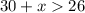
Solving the inequalities gives:
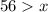
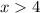
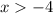
Combining the solutions we get:
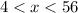
Therefore, the length of the third side of the triangle could be 4.5 units.