Question

Plot the x-intercepts, y-intercepts, vertex, and axis of symmetry for the function G.

G(x)=x^2+4x+3

Answer 1

x-intercepts: (-3, 0) and (-1, 0)

y-intercept: (0, 3)

Vertex: (-2, -1)

Axis of symmetry: x = -2

Explanation:

x-intercepts

The x-intercepts of a function are the points at which the graph crosses the x-axis. At these points, the value of the function (y-value) is equal to zero, y = 0.

Therefore, to find the x-intercepts of the given function g(x), set the function to zero and solve for x:

`\begin{aligned}g(x)&=0\\x^2+4x+3&=0\\x^2+x+3x+3&=0\\x(x+1)+3(x+1)&=0\\(x+3)(x+1)&=0\\\\x+3&=0 \implies x=-3\\x+1&=0 \implies x=-1\end{aligned}`

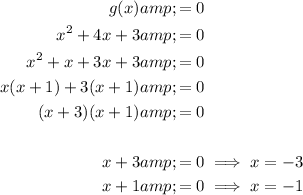
Therefore, the x-intercepts of function g(x) are (-3, 0) and (-1, 0).

`\hrulefill`

y-intercept

The y-intercept of a function is the point at which the graph crosses the y-axis. At this point, the value of the function (x-value) is equal to zero, x = 0.

Therefore, to find the y-intercept of the given function g(x), substitute x = 0 into the function and solve:

`\begin{aligned}x=0 \implies g(0)&=(0)^2+4(0)+3\\&=0+0+3\\&=3\end{aligned}`

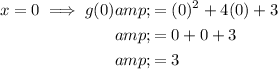
Therefore, the y-intercept of function g(x) is (0, 3).

`\hrulefill`

Vertex

The vertex of a quadratic function is the point on the graph of the function where the parabola reaches its maximum or minimum value

The x-value of the vertex of a quadratic function is the midpoint between the two x-intercepts. The x-intercepts of function g(x) are -3 and -1. Therefore, the x-value of the vertex is x = -2.

To find the y-value of the vertex, substitute the found x-value into the given function:

`\begin{aligned}x=-2 \implies g(-2)&=(-2)^2+4(-2)+3\\&=4-8+3\\&=-1\end{aligned}`

Therefore, the vertex of function g(x) is (-2, -1).

`\hrulefill`

Axis of symmetry

The axis of symmetry of a function is a vertical line that divides the graph into two symmetric halves. The axis of symmetry of a quadratic function is located at the x-value of the vertex.

Therefore, since the x-value of the vertex is -2, the axis of symmetry of function g(x) is x = -2.