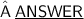
The given system of equations is:

To solve this system, we can use the method of elimination or substitution. Let's use the method of elimination:
First, we'll multiply the first equation by 2 to make the coefficients of
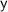 in both equations equal:
in both equations equal:

Now, we can subtract the second equation from the first equation to eliminate the variable
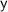 :
:
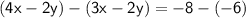
Simplifying the expression:
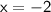
Now that we have found the value of
 , we can substitute it back into either of the original equations to solve for
, we can substitute it back into either of the original equations to solve for
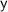 . Let's substitute it into the first equation:
. Let's substitute it into the first equation:

Simplifying the expression:
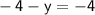
Solving for
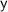 :
:

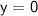
Hence, the solution to the system of equations is
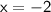 and
and
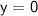 .
.

♥️
