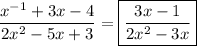Question

Simplify fully.

X^-1 +3x-4
—————
2x²-5x+3

Answer 1

`(3x-1)/(2x^2-3x)`

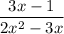
Explanation:

Given rational expression:

`(x^(-1)+3x-4)/(2x^2-5x+3)`

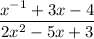
First, we need to eliminate the negative exponent in the numerator.

To do this, multiply the numerator by x / x:

`\begin{aligned}(x^(-1)+3x-4) \cdot (x)/(x)&=( x^(-1)\cdot x+3x\cdot x-4 \cdot x)/(x)\\\\&=(1+3x^2-4x)/(x)\end{aligned}`

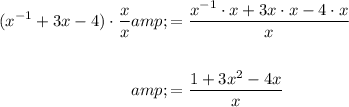
Therefore:

`(x^(-1)+3x-4)/(2x^2-5x+3)=((1+3x^2-4x)/(x))/(2x^2-5x+3)`

`\textsf{Apply\:the\:fraction\:rule:}\:((a)/(b))/(c)=(a)/(b\cdot \:c)`

`=(1+3x^2-4x)/(x\cdot (2x^2-5x+3))`

`=(3x^2-4x+1)/(x(2x^2-5x+3))`

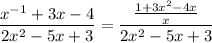
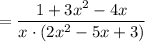
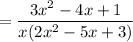
Factor the quadratics in the numerator and the denominator:

`\begin{aligned}\textsf{Numerator:}\quad 3x^2-4x+1&=3x^2-3x-x+1\\&=3x(x-1)-1(x-1)\\&=(3x-1)(x-1)\end{aligned}`

`\begin{aligned}\textsf{Denominator:}\quad 2x^2-5x+3&=2x^2-2x-3x+3\\&=2x(x-1)-3(x-1)\\&=(2x-3)(x-1)\end{aligned}`

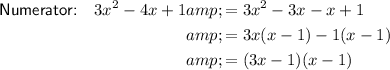
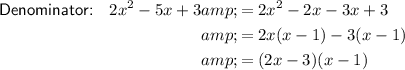
Therefore:

`(x^(-1)+3x-4)/(2x^2-5x+3)=((3x-1)(x-1))/(x(2x-3)(x-1))`

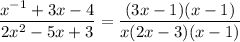
Factor out the common term (x - 1):

`=(3x-1)/(x(2x-3))`

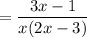
Simplify the denominator:

`=(3x-1)/(2x^2-3x)`

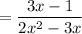
Therefore:

`(x^(-1)+3x-4)/(2x^2-5x+3)=\boxed{(3x-1)/(2x^2-3x)}`