Find the radius of the base of a container that is 28 centimeters tall and has a volume of 8,800 cubic centimeters. (Use π = 3 1/7.)

Question

asked Nov 7, 2024 2.8k views

1 Answer

Hien Nguyen · Answer 1 · 2024-11-11T19:25:42+0000

Required answer:

Explanation:

Shape of container is cylinder

As per the question we have been given volume of the container 8,800 cubic centimeters and the container that is 28 centimeters tall.

Formula :

$\pi = 3 (1)/(7) \\ \\ \pi = (22)/(7)$

Plugging the values of height, π and volume in the above formula :

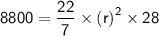
$\sf8800 = (22)/(7) * {(r)}^(2) * 28$

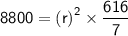
$\sf8800 = {(r)}^(2) * (616)/(7)$

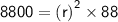
$\sf8800 = {(r)}^(2) * 88$

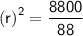
$\sf {(r)}^(2) = (8800)/(88)$

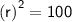
$\sf {(r)}^(2) = 100$

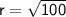
$\sf r = √(100)$

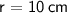
$\sf \ r = 10 \: cm$

So the radius of the base of a container is 10 cm