Question

A ladder resting on a vertical wall makes an angle whose tangent is 2.4 with the ground. If the distance between the foot of the ladder and the wall is 50cm, what is the length of the ladder?​

Answer 1

`\dag \: \: \: \huge{ \boxed{ \sf{ \pink{A\green{N \blue{S\color{yellow}W\red{E\orange{R}}}}}}}}`

Given:

Angle
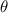`\displaystyle\sf \theta` (angle between the ladder and the ground):
`\displaystyle\sf \tan(\theta) = 2.4`

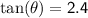
Distance between the foot of the ladder and the wall:
`\displaystyle\sf d = 50\,cm`

To find:

Length of the ladder:
`\displaystyle\sf x`

Using the tangent function:

`\displaystyle\sf \tan(\theta) = \frac{{\text{{opposite}}}}{{\text{{adjacent}}}}`

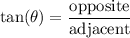
In this case:

Opposite side is the height of the wall:
`\displaystyle\sf x`

Adjacent side is the distance between the foot of the ladder and the wall:
`\displaystyle\sf d`

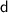
So we have:

`\displaystyle\sf \tan(\theta) = \frac{{x}}{{d}}`

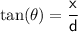
Substituting the given values:

`\displaystyle\sf 2.4 = \frac{{x}}{{50}}`

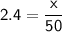
To find
`\displaystyle\sf x`, we can solve for it by multiplying both sides of the equation by 50:

`\displaystyle\sf 2.4 * 50 = x`

Simplifying:

`\displaystyle\sf x = 120`

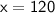
Therefore, the length of the ladder is 120 cm.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`