Question

four children are told to line up and hold hands as they cross the street. how many different ways can they line up

Answer 1

If the four children are asked to line up and hold hands, then the number of ways they can line up is the same as the number of permutations of four objects, which is 4 factorial or 4! = 4 x 3 x 2 x 1 = 24.

Answer 2

The answer is:

24 ways

Work/explanation:

To find how many different ways the children can line up, we will find the factorial of 4 (because there are 4 children).

The factorial of 4 simply means we multiply it by itself, then the numbers that are less than 4 (these numbers are nonzero and non-negative).

The factorial is denoted as x!.

So now, we calculate the factorial of 4:

`\sf{4!=4*3*2*1}`

`\sf{4!=24}`

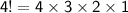
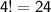
Hence, the answer is 24.