Question

A line passes through the point (-6, 6) and (-6, 2). in two or more complete sentences, explain why it is not possible to write the equation of the given line in the traditional version of the point-slope form of a line. type your answer in the box provided to submit your solution.

Answer 1

The answer is:

Below

Work/explanation:

Let's begin by taking a look at the traditional point slope form.

`\pmb{y-y_1=m(x-x_1)}`

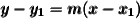
where m = slope and (x1, y1) is a point.

The problem is, when we try to find the slope using the slope formula, we end up with the following answer:

`\sf{m=(y_2-y_1)/(x_2-x_1)}`

`\sf{m=(2-6)/(-6-(-6))}`

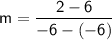
We know that -6 - (-6) simplifies to -6 + 6

`\sf{m=(-4)/(-6+6)}`

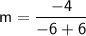
Now here's the catch:

`\sf{m=(-4)/(0)}`

`\sf{m=un de fined}`

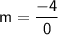
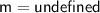
In summary, we can't write the equation of this line in point slope, because its slope is undefined. Remember that for point slope, we need the slope, but since it's not defined, we can't plug it into point slope.