Answer:

Explanation:
In order to solve this problem, we have to use the formula for the area of a circle:
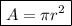
where:
A ⇒ area of the circle = 16 m²
r ⇒ radius of the circle
Since we already know the area of the circle, we can substitute the given value into the formula above and then solve for r to get the radius of the circle:
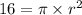
⇒
 [Dividing both sides of the equation by π]
[Dividing both sides of the equation by π]
⇒
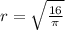 [Taking the square root of both sides of the equation]
[Taking the square root of both sides of the equation]
⇒
 [Distributing the square root]
[Distributing the square root]
⇒
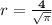
It is usually encouraged to remove the square root from the denominator of a fraction. To do this we can multiply both the numerator and the denominator by the square root:

⇒

Therefore, the correct answer is A.