Question

The answer for the question I provided

Answer 1

7x

Explanation:

Suppose that,
`\displaystyle{e^(\ln ax) = ax}`, let's prove that the following equation is true for all possible x-values (identity).

First, apply the natural logarithm (ln) both sides:

`\displaystyle{\ln \left( e^(\ln ax) \right)=\ln \left(ax\right)}`

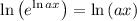
From the property of the logarithm -
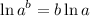`\displaystyle{\ln a^b = b\ln a}`. Therefore,

`\displaystyle{\ln ax \cdot \ln e = \ln ax}`

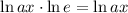
ln(e) = 1, so:

`\displaystyle{\ln ax \cdot 1 = \ln ax}\\\\\displaystyle{\ln ax = \ln ax}`

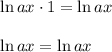
Hence, this is true. Thus,
`\displaystyle{e^(\ln ax) = ax}`, and
`\displaystyle{e^(\ln 7x) = 7x}`.