Question

The line (y-2)= (2/7)(x-1) contains point (a, 4) . What is the value of a ?

Answer 1

a = 8

Explanation:

The question has given us the following equation of a line:

`y-2= (2)/(7)(x-1)`,

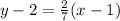and told us that it contains the point (a, 4). It then asks us to find the value of a.

To do this, we have to understand the following: since point (a, 4) is on the given line, these coordinates satisfy the equation of the line. In other words, if we substitute the given values into the equation, the equality will still be valid.

Therefore, we can simply substitute (a, 4) into the equation and then solve for a:

`y-2= (2)/(7)(x-1)`

⇒
`4 - 2 = (2)/(7)(a-1)`

⇒
`2 = (2)/(7)(a - 1)`

⇒
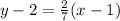
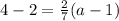
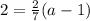
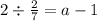`2 / (2)/(7) = a - 1` [Dividing both sides of the equation by
`(2)/(7)`]

⇒
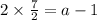`2 * (7)/(2) = a-1` [Dividing by a fraction is the same as multiplying by its reciprocal]

⇒
`(14)/(2) = a - 1`

⇒
`7= a - 1`

⇒
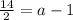
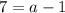
`a = 7 + 1` [Adding 1 to both sides]

⇒
`a = \bf 8`

Therefore, the value of a is 8.