The answer is:
y = 3x + 2
Work/explanation:
If two lines are parallel to each other, their slopes are equal.
Consider the given equation, y = 3x - 1. Its slope is 3. Hence, the slope of the line that is parallel to y = 3x - 1 is 3.
So far, the equation is y = 3x + b.
Now, there are two ways we could find b. We could use point slope, and simplify to slope intercept, or, we could plug the point directly into the equation y = 3x + b, and solve for b. Allow me to demonstrate both ways.

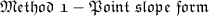
The equation is
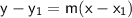 , where m = slope and (x₁,y₁) is a point on the line.
, where m = slope and (x₁,y₁) is a point on the line.
Plug in the data

Simplify

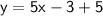
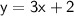
Hence, the equation is y = 3x + 2. Now I will use the second method, and see if I obtain the same answer!


Plug the point (1,5) directly into the equation y = 3x + b; plug in 1 for x, and 5 for y.
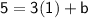
Simplify
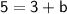
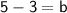
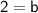
Hence, the y intercept is 2; and the equation is y = 3x + 2.
As you can see, I have used two different ways, and I have arrived at the same answer.