Answer:
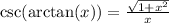
Domain is
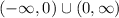
Explanation:
Let
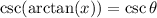 so that
so that
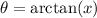 and
and
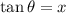 :
:
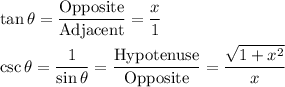
You can get these values by drawing a right triangle and labeling each side. Hypotenuse is easily calculated with the Pythagorean Theorem.
Now that we know
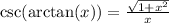 , it's clear that
, it's clear that
 , so the domain of the composite trig function is
, so the domain of the composite trig function is
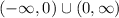 .
.