1. What passes through (-8,6) and is parallel to
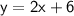
To find a line parallel to
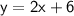 passing through
passing through
 , we can use the slope-intercept form of a line
, we can use the slope-intercept form of a line
 , where
, where
 is the slope and
is the slope and
 is the y-intercept.
is the y-intercept.
Since the given line
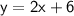 has a slope of
has a slope of
 , any line parallel to it will have the same slope. Therefore, the line passing through
, any line parallel to it will have the same slope. Therefore, the line passing through
 and parallel to
and parallel to
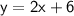 can be represented as
can be represented as
 , where
, where
 is the y-intercept we need to determine.
is the y-intercept we need to determine.
To find
 , substitute the coordinates of the point
, substitute the coordinates of the point
 into the equation:
into the equation:
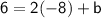
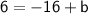
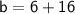
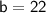
Therefore, the equation of the line passing through
 and parallel to
and parallel to
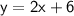 is
is
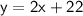 .
.
2. What passes through (4,-1) and is perpendicular to

To find a line perpendicular to
 passing through
passing through
 , we know that the slopes of perpendicular lines are negative reciprocals of each other.
, we know that the slopes of perpendicular lines are negative reciprocals of each other.
The given line
 has a slope of
has a slope of
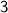 . The negative reciprocal of
. The negative reciprocal of
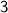 is
is
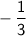 .
.
Using the point-slope form of a line
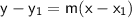 , where
, where
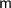 is the slope and
is the slope and
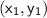 are the coordinates of a point on the line, we can substitute
are the coordinates of a point on the line, we can substitute
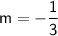 and
and
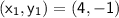 into the equation.
into the equation.
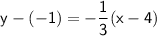
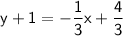
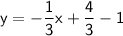
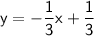
Therefore, the equation of the line passing through
 and perpendicular to
and perpendicular to
 is
is
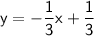 .
.
3. What passes through (9,-5) and is vertical
A vertical line has an undefined slope and is of the form
 , where
, where
 is a constant.
is a constant.
Since the line passes through
 , the equation of the vertical line can be written as
, the equation of the vertical line can be written as
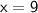 .
.
Therefore, the equation of the line passing through
 and is vertical is
and is vertical is
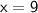 .
.
4. What passes through (-2,7) and is horizontal
A horizontal line has a slope of 0 and is of the form
 , where
, where
 is a constant.
is a constant.
Since the line passes through
 , the equation of the horizontal line can be written as
, the equation of the horizontal line can be written as
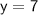 .
.
Therefore, the equation of the line passing through
 and is horizontal is
and is horizontal is
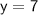 .
.

♥️
