High points rewarded for this question and need help please

Question

asked Jul 16, 2024 209k views

1 Answer

DanKodi · Answer 1 · 2024-07-21T21:43:00+0000

$\Large{\boxed{\sf A_(shaded \: shape) = 55cm^2}}$

$\\$

The shaded area corresponds to the area of the trapezoid, from which we subtract the area of the rectangle.

$\\ \\$

$\\ \\$

The area of a trapezoid is given by the following formula:

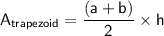
$\sf A_(trapezoid) = ((a + b))/(2) * h$

Where:

$\\$

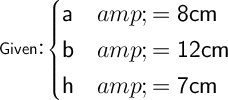
$\sf \Large{\sf Given \text{:} \begin{cases} \sf a &=\sf 8cm \\ \sf b &=\sf 12cm \\ \sf h &= \sf 7cm \end{cases} }$

$\\$

Substituting these values into our formula, we get:

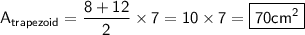
$\sf A_(trapezoid) = (8 + 12)/(2) * 7 = 10 * 7 = \boxed{\sf 70cm^2}$

$\\ \\$

$\\ \\$

We can calculate the area of a rectangle using the following formula:

$\sf A_(rectangle) = L * W$

Where:

$\\$

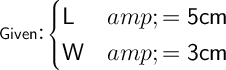
$\sf \Large{\sf Given \text{:} \begin{cases} \sf L &=\sf 5cm \\ \sf W &=\sf 3cm \end{cases} }$

$\\$

Substitute these values into our formula:

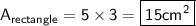
$\sf A_(rectangle) = 5 * 3 = \boxed{\sf 15cm^2}$

$\\ \\$

We can now find the area of the shaded shape:

$\sf A_(shaded \: shape) = A_(trapezoid) - A_(rectangle) = 70 - 15 = \boxed{\boxed{\sf 55cm^2}}$