Question

a gray kangaroo can bound across a flat stretch of ground with each jump carrying it 10m from the takeoff point if the kangaroo leaves the ground at 20 degree angle, what its take off speed and horizontal speed

Answer 1

The take-off velocity of the kangaroo would be
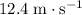`12.4\; {\rm m\cdot s^(-1)}` at the
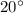`20^(\circ)` angle above horizon (assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`.)

The horizontal speed of the kangaroo would be approximately
`11.6\; {\rm m\cdot s^(-1)}`.

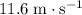Step-by-step explanation:

Let
`u` denote the initial take-off speed of the kangaroo. To find the value of
`u`, start by finding expressions for the horizontal speed of the kangaroo and the duration of the jump- both in terms of
`u\!`. After that, solve for
`u\!\!` by constructing an equation for the horizontal distance that the kangaroo travelled during the jump.

Let
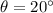`\theta = 20^(\circ)` denote the angle of elevation of the take-off velocity of the kangaroo above the horizon.

• Initial vertical velocity of the kangaroo would be
  `u_(y) = u\, \sin(\theta)`.
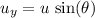• Initial horizontal velocity of the kangaroo would be
  `u_(x) = u\, \cos(\theta)`.

During the jump, the vertical velocity of the kangaroo would be changing at at an acceleration of
`a_(y) = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}`. The horizontal velocity of the kangaroo would stay constant.

Right before the kangaroo lands, its vertical velocity would be the opposite of that when it took off:
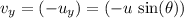`v_(y) = (- u_(y)) = (-u\, \sin(\theta))`. The change in vertical velocity would be:

`\begin{aligned} \Delta v_(y) &= (v_(y) - u_(y)) \\ &= (-u\, \sin(\theta)) - u\, \sin(\theta) \\ &= 2\, u\, \sin(\theta) \end{aligned}`.

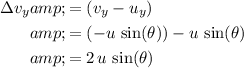Divide the change in vertical velocity
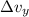`\Delta v_(y)` by vertical acceleration
`a_(y)` (the rate of change in velocity) to find an expression for the duration
`t` of the jump:

`\begin{aligned}t &= (\Delta v_(y))/(a_(y)) \\ &= (-2\, u\, \sin(\theta))/(-g) \\ &= (2\, u\, \sin(\theta))/(g)\end{aligned}`.

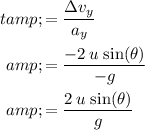Since the horizontal velocity
`u_(x)` of the kangaroo stays the same throughout the jump, the distance travelled during the jump can be found by multiplying this velocity by the duration of the jump:

`\begin{aligned} s &= u_(x)\, t \\ &= (u\, \cos(\theta))\, (2\, u\, \sin(\theta))/(g) \\ &= (2\, u^(2)\, \sin(\theta)\, \cos(\theta))/(g)\end{aligned}`.

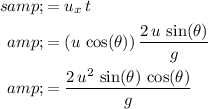It is given that the horizontal distance travelled during the jump is
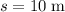`s = 10\; {\rm m}`. Additionally,
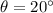`\theta = 20^(\circ)` while
`g = 9.81\; {\rm m\cdot s^(-2)}`. Rearrange the expression for
`s` to find initial velocity
`u`:

`\begin{aligned}u &= \sqrt{(s\, g)/(2\, \sin(\theta)\, \cos(\theta))} \\ &\approx \sqrt{((10)\, (9.81))/(2\, \sin(20^(\circ))\, \cos(20^(\circ)))}\; {\rm m\cdot s^(-1)} \\ &\approx 12.4\; {\rm m\cdot s^(-1)}\end{aligned}`.

Substitute this value into the expression for the horizontal velocity of the kangaroo to obtain the value of horizontal velocity:

`\begin{aligned} u_(x) &= u\, \cos(\theta) \\ &\approx 12.3538\, \cos(20^(\circ)) \\ &\approx 11.6\; {\rm m\cdot s^(-1)} \end{aligned}`.