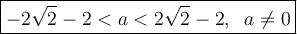Question

Find all possible values of a such that ax² + (2a + 2)x + a + 3 = 0 has two roots and the distance between them on the number line is greater than 1.​

Answer 1

The answer I think is 0

Answer 2

`-2√(2)-2 < a < 2√(2)-2,\;\;a\\eq0`

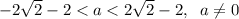
Explanation:

Given quadratic equation:

`ax^2 + (2a + 2)x + a + 3 = 0`

To find the possible values of "a" such that the given equation has two roots and the distance between them on the number line is greater than 1, use the quadratic formula.

`\boxed{\begin{minipage}{4 cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\\\\when $ax^2+bx+c=0$ \\\end{minipage}}`

Comparing the coefficients:

• 
  `a = a`
• 
  `b = (2a + 2)`
• 
  `c = (a + 3)`

Substitute the coefficients into the quadratic formula:

`x=(-(2a+2) \pm √((2a+2)^2-4a(a + 3)))/(2a)`

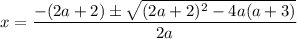
Simplify the discriminant (the part under the square root sign):

`x=(-(2a+2) \pm √(-4a+4))/(2a)`

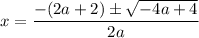
Factor out 4 from the discriminant:

`x=(-(2a+2) \pm √(4(-a+1)))/(2a)`

`\textsf{Apply the radical rule:} \quad √(ab)=√(a)√(b)`

`x=(-(2a+2) \pm √(4)√(-a+1))/(2a)`

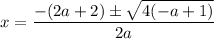
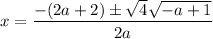
Therefore:

`x=(-(2a+2) \pm 2√(-a+1))/(2a)`

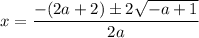
Factor out the common term 2:

`x=(-(a+1)\pm √(-a+1))/(a)`

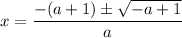
Therefore, the two solutions are:

`x=(-a-1+√(-a+1))/(a),\;\;x=-(a+1+√(-a+1))/(a)`

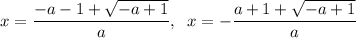
As both solutions have "a" as their denominator, a ≠ 0.

Note: When substituting a = 0 into the original equation, we are left with a linear equation, which only has one root. Therefore, this confirms that a ≠ 0.

Now we have found expressions for the two roots, we can set the distance between them to greater than 1:

`(-a-1+√(-a+1))/(a)-\left(-(a+1+√(-a+1))/(a)\right) > \:1`

`(-a-1+√(-a+1))/(a)+(a+1+√(-a+1))/(a) > \:1`

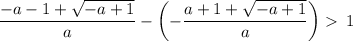
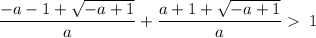
Simplify:

`\begin{aligned}(-a-1+√(-a+1)+a+1+√(-a+1))/(a)& > 1\\\\(2√(-a+1))/(a)& > 1\\\\2√(-a+1)& > a\\\\(2√(-a+1))^2& > a^2\\\\4(-a+1)& > a^2\\\\-4a+4& > a^2\\\\a^2+4a-4& < 0\\\\(a+2)^2-8& < 0\\\\(a+2)^2& < 8\end{aligned}`

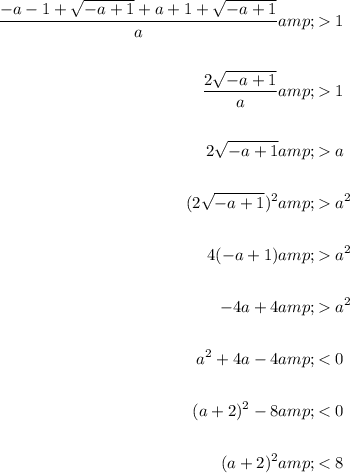
`\textsf{For\;\;$u^n < a$,\;\;if\;$n$\;is\;even\;then\;\;$-\sqrt[n]{a} < u < \sqrt[n]{a}|$:}`

`-√(8) < a+2 < √(8)`

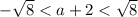
Therefore:

`-√(8) -2 < a < √(8)-2`

`-2√(2)-2 < a < 2√(2)-2`

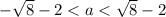
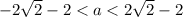
So the possible values of "a" such that ax² + (2a + 2)x + a + 3 = 0 has two roots and the distance between them on the number line is greater than 1 are:

`\large{\boxed{-2√(2)-2 < a < 2√(2)-2,\;\;a\\eq0}`