Question

Solve the system of equations any way you wish. Show all your work.

xy = −2
y = x + 3

Answer 1

The answer is:

`\sf{x=-1,y=2}`

`\sf{x=-2,y=1}`

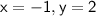
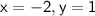
Work/explanation:

We know that y = x + 3, so we can plug that into the first equation:

`\sf{xy=-2}`

`\sf{x(x+3)=-2}`

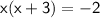
That way, we only have one variable. Now, distribute x:

`\sf{x^2+3x=-2}`

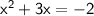
Add 2 on each side, so that the right side is 0.

`\sf{x^2+3x+2=0}`

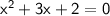
Now think of two numbers whose sum is 3, and whose product is 2.

These numbers are 2 and 1.

2 * 1 = 2;

2 + 1 = 3.

All good here! Moving on to the next step.

So now we write the equation as,

`\sf{(x+1)(x+2)=0}`

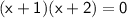
Now we have 2 little equations that can be solved;

x + 1 = 0

x + 2 = 0

Solving,

x = -1

x = -2

Now, we still need to find y, so we plug in both values of x into the equation y = x + 3.

`\sf{y=-1+3}`

`\sf{y=2}`

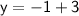
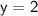
Plug in the value of the second x:

`\sf{y=-2+3}`

`\sf{y=1}`

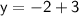
Hence, the answer to the system

`\begin{cases}\bf{xy=-2}\\\bf{y=x+3}\end{cases}}`

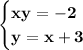
is:

x = -1, y = 2

x = -2, y = 1