Question

Quadrilateral OPQR is inscribed inside a circle as shown below. What is the measure of angle O? You must show all work

and calculations to receive credit.
O = (2x)°
P = y°
Q = (2x+4)°
R = (3y+8)°

Answer 1

∠O = 88

Explanation:

Since OPQR is inscribed in a circle, OPQR is a cyclic quadrilateral.

By property, the opposite angles in a cyclic quadrilateral add up to 180°

⇒ ∠O + ∠Q = 180
⇒ 2x + 2x + 4 = 180

⇒ 4x + 4 = 180

⇒ 4x = 180 - 4

⇒ 4x = 176

⇒ x =
`(176)/(4)`

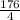
⇒ x = 44

∠O = 2x

⇒ ∠O = 2 * 44

⇒ ∠O = 88

Note: I have assumed an image and attached it. But either way, even if the image in your question looks different, the angles will be the same and ∠O and ∠Q will still be opposite angles