Answer:
(-14/15, -114/45)
Explanation:
The shortest distance between a given point and a line is the perpendicular segment from the closest point on the line to that given point. Therefore, if we get the given equation to be in slope-intercept form and then find the line perpendicular to it that also passes (0,-3), we'll be able to see what the closest point is.
Original line in slope-intercept form
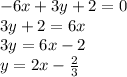
Perpendicular line that passes through (0,-3)
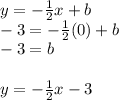
Find where both lines intersect
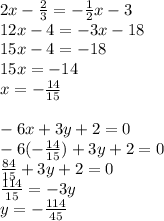
Therefore, the point on the line -6x + 3y + 2 = 0 which is closest to the point (0,-3) would be (-14/15, -114/45).