Answer:
Explanation:
6) The inequalities are
x + y ≥ 60
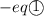
400x + 1200y ≤ 68000

y ≥ 3x
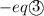
x ≥ 0
y ≥ 0
P = 1900x + 14500y
7)
Intersection of eq(1) and eq(2)
x + y ≥ 60
⇒ y ≥ 60 - x
sub in eq(2)
400x + 1200(60 - x) = 68000
⇒ 400x + 72000 - 1200x = 68000
⇒ 72000 - 68000 = 1200x - 400x
⇒ 4000 = 800x
⇒ x = 4000/800
⇒ x = 5
sub in y ≥ 60 - x
y ≥ 60 - 5
y ≥ 55
Point1 (5, 55)
Intersection of eq(1) and eq(3)
x + y ≥ 60
y ≥ 3x
sub (3) in (1)
x + (3x) = 60
⇒ 4x = 60
⇒ x = 60/4
⇒ x = 15
sub in y ≥ 3x
y ≥ 3(15)
y ≥ 45
Point2 (15, 45)
Intersection of eq(2) and eq(3)
400x + 1200y ≤ 68000
y ≥ 3x
sub (3) in (2)
400x + 1200(3x) = 68000
⇒ 400x + 3600x = 68000
⇒ 4000x = 68000
⇒ x = 68000/4000
⇒ x = 17
y ≥ 3x
y ≥ 3(17)
y ≥ 51
Point3 (17, 51)
The three vertices are (5, 55), (15, 45) and (15, 45)
8) P = 1900x + 14500y
at Point1, P = 1900(5) + 14500(55) = 807000
at Point2, P = 1900(15) + 14500(45) = 681000
at Point3, P = 1900(17) + 14500(51) = 771800
The maximum is: P = 807000 when x = 5 and y = 55
9) The maximum number of people exposed to the ad is 807000, when there are 5 radio ads and 55 tv ads