Question

Pls answer quickly

Due in 2 mins

(08.02)How many solutions are there for the system of equations shown on the graph?


A coordinate plane is shown with two lines graphed. One line crosses the y axis at 3 and has a slope of negative 1. The other line crosses the y axis at 3 and has a slope of two thirds.

Answer 1

To find the number of solutions for the system of equations shown on the graph, we need to find the point where the two lines intersect. The two lines are:

- Line 1: y = -x + 3

- Line 2: y = (2/3)x + 3

To find the point where these two lines intersect, we can set the two equations equal to each other and solve for x:

- -x + 3 = (2/3)x + 3

- -x - (2/3)x = 0

- -(5/3)x = 0

- x = 0

Now that we know x = 0, we can substitute this value into either equation to find y:

- y = -x + 3

- y = -0 + 3

- y = 3

Therefore, the point where the two lines intersect is (0, 3). Since there is only one point of intersection between the two lines, there is **one solution** for the system of equations shown on the graph.

I hope this helps!

Answer 2

One solution

Explanation:

The slope-intercept form of a linear equation is y = mx + b, where m is the slope, and b is the y-intercept.

From the given description, the system of equations of the two lines is:

`\begin{cases}y=-x+3\\\\y=(2)/(3)x+3\end{cases}`

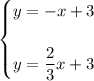
The lines have different slopes, therefore they will intersect at one point. The point of intersection is the solution of the system of equations.

To find the point of intersection, solve the system of equations by the method of substitution:

`\begin{aligned}(2)/(3)x+3&=-x+3\\\\(2)/(3)x+3-3&=-x+3-3\\\\(2)/(3)x&=-x\\\\(2)/(3)x+x&=-x+x\\\\ (5)/(3)x&=0\\\\x&=0\end{aligned}`

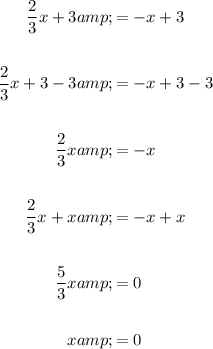
Substitute the found value of x into one of the equations:

`y=-x+3`

`y=-(0)+3`

`y=3`

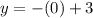
Therefore, the point of intersection, and therefore the solution, of the system of equations is (0, 3). This confirms that there is one solution.