Question

What is the vertex form of y=4x^2+16x-48 ?

Please include the steps as well! :)

Answer 1

Explanation:

For a parabola in the form,

`y=ax^(2) +bx+c`

The vertex form of a parabola is

`y=a(x-h)^(2) +k`

where (h,k) is the vertex.

`h=(-b)/(2a)`

`k=f(h)`

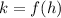
So basically, to find the value of h, just multiply the b value of the parabola by -1, and then divide it by 2 times a value.

To find the k value, substitute the h value into the original function.

Here

a=4

b=16

c=-48

So,

`h=(-16)/(2(4)) =-2\\k= f(-2)= 4(-2)^(2) +16(-2)-48= 16-32-48=-64\\`

So the equation in vertex form is.

`y=4(x+2)^(2) -64`