Question

Please help I am so lost thank you all

Answer 1

x = number of radio ads

y = number of TV ads

x and y are nonnegative whole numbers (0,1,2,3,...) which means that both
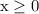`\text{x} \ge 0` and
`\text{y} \ge 0`

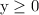
x+y = total number of ads purchased

This total must be 60 or more due to the phrasing "they plan to purchase at least 60 total ads". We will form the inequality
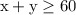`\text{x}+\text{y} \ge 60` and that solves to
`\text{y} \ge -\text{x}+60`

-------------------

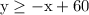
1 radio ad costs $400, so x of them will cost 400x dollars.

1200y = cost of all the TV ads

400x+1200y = total cost

This total cost must be $68,000 or smaller to keep under budget.

We arrive at
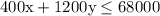`400\text{x}+1200\text{y} \le 68000` which is the same as
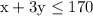`\text{x}+3\text{y} \le 170` and solves to
`\text{y} \le -(1)/(3)\text{x}+170`

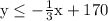
Another inequality is
`\text{y} \ge 3\text{x}` because we want at least 3 times as many TV ads compared to radio.

-------------------

Let's recap so far.

We have this system of inequalities

`\begin{cases}\text{x}+\text{y} \ge 60\\400\text{x}+1200\text{y} \le 68000\\\text{y} \ge 3\text{x}\\\text{x} \ge 0\\\text{y} \ge 0\end{cases}`

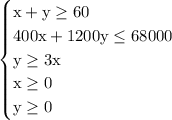
which is equivalent to this system

`\begin{cases}\text{y} \ge -\text{x}+60\\\text{y} \le -(1)/(3)\text{x}+170\\\text{y} \ge 3\text{x}\\\text{x} \ge 0\\\text{y} \ge 0\end{cases}`

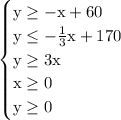
The idea from here is to plot each boundary line associated with those inequalities shown above.

For instance, the boundary equation for
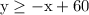`\text{y} \ge -\text{x}+60` would be
`\text{y} = -\text{x}+60`

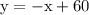
Desmos is useful to quickly plot such an equation. Plot the other equations
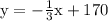`\text{y} = -(1)/(3)\text{x}+170` and
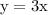`\text{y} = 3\text{x}` on the same xy grid.

We'll then shade above the line y = -x+60 because of the "greater than" symbol associated with this corresponding inequality. The same goes for y = 3x. The other inequality has "less than" to mean we shade below that boundary.

The shaded region is inside a triangle which forms the 3 vertices we need.

The vertex points are:

• (5,55)
• (15,45)
• (17,51)

Refer to the diagram below. Each corner point is a result of solving a system of exactly two equations. For instance, solve this system

`\begin{cases}\text{y} = -(1)/(3)\text{x}+170\\\text{y} = 3\text{x}\end{cases}`

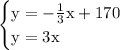
and the solution is the point (17,51) meaning x = 17 and y = 51. Use substitution to solve.

-------------------

We're then given the info that "It is estimated that each radio ad will be heard by 1900 listeners" and also "each TV ad will be seen by 14500 people".

1 radio ad = 1900 people

x radio ads = 1900x people

1 TV ad = 14500 people

y TV ads = 14500y people

1900x+14500y = total people reached by both types of ads combined

The goal is to max out how many people are reached.

To find when 1900x+14500y is maxed out, we plug each of those corner points into that expression.

Let's try (5,55)

1900x+14500y

1900*5+14500*55

807000

This means purchasing 5 radio and 55 TV ads will reach 807,000 total people. This is an estimate.

Now try (15,45)

1900x+14500y

1900*15+14500*45

681000

The number has gone down from its previous value (807000), which means it's not a good idea to go for this corner point compared to the first one mentioned.

The last one to check is the corner (17,51)

1900x+14500y

1900*17+14500*51

771800

This result isn't larger than 807000, so the first corner point is the best one to go for. It makes 1900x+14500y as large as possible while keeping within the constraints set up with the inequalities.