Answer:
y = -3x + 7
Explanation:
Pre-Solving
We are given that a line passes through the point (3, -2) and has a slope of -3.
We want to write the equation of this line, and there are three ways to do so:
- Slope-intercept form, which is y=mx+b where m is the slope and b is the value of y at the y-intercept.
- Standard form, which is ax+by=c where a, b, and c are free integer coefficients.
- Slope-point form, which is
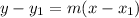 where m is the slope and
where m is the slope and
 is a point.
is a point.
Since the question doesn't specify which form we should write the answer in, we can use any one of the forms.
Let's write the equation in slope-intercept form, as it is the most popular way to write the equation of the line.
Solving
As we already know the slope of the line, we can plug it into the formula.
y = mx + b
y = -3x + b
Now, we need to find b.
As the line passes through (3, -2), we can use its values to help solve for b.
Substitute 3 as x and -2 as y.
-2 = -3(3) + b
Multiply.
-2 = -9 + b
Add 9 to both sides.
7 = b
Substitute 7 as b in the equation.
y = -3x + 7
The equation of the line is y = -3x + 7.