keeping in mind that parallel lines have exactly the same slope, let's check for the slope of the line above. To get the slope of any straight line, we simply need two points off of it, and we have three, let's use two of those
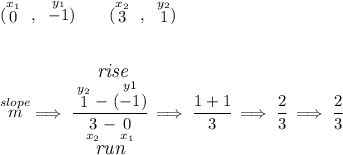
any line parallel to that will then have the exact same slope, so we're really looking for the equation of line whose slope is 2/3 and it passes through the x-intercept at -3.
