Question

The first three terms of a sequence are given. Round to the nearest thousandth (if

necessary).
2, 7, 12,...
Find the 46th term.

Answer 1

Answer: 227

Explanation:

To find the 46th term of the sequence, we need to first determine the pattern of the sequence. We can see that the sequence increases by 5 between each consecutive term. Therefore, the common difference of the sequence is 5.

Using this information, we can find the
`n`th term of the sequence using the formula:

`\Large \boxed{an = a1 + d(n-1)}`

where

• 
  `an = \text{nth term of the sequence}`

• 
  `a1 = \text{first term of the sequence}`

• 
  `d = \text{common difference}`

Using the given terms, we have:

• 
  `a1 = 2`

• 
  `d = 5`

To find the 46th term, we substitute
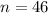`n = 46` into the formula:

• 
  `a46 = 2 + 5(46-1)`

• 
  `a46 = 2 + 225`

• 
  `a46 = 227`

Therefore, the 46th term of the sequence is 227.

________________________________________________________

Answer 2

To find the pattern in the sequence, we can observe that each term is obtained by adding 5 to the previous term. Therefore, we can write the recursive formula for the sequence as:

`\large a_1 = 2`

`\large a_n = a_(n-1) + 5`

To find the 46th term, we can use the recursive formula to generate each term until we reach the desired term:

`\large a_1 = 2`

`\large a_2 = a_1 + 5 = 2 + 5 = 7`

`\large a_3 = a_2 + 5 = 7 + 5 = 12`

`\large a_4 = a_3 + 5 = 12 + 5 = 17`

`\vdots`

`\large a_(46) = a_(45) + 5 \approx \boxed{227}`

`\therefore` The 46th term of the sequence is approximately 227.

We can also write the explicit formula for the sequence as:

`\large a_n = 5n - 3`

To verify that this formula generates the same sequence as the recursive formula, we can substitute the value of n = 1, 2, 3, etc. and compare the results.

`\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}`