Question

Solve the equation: x²-2x=8
Show all the Steps with explanation.​

Answer 1

x = 4, -2

Explanation:

x^2-2x=8

Move the constant term to the right side of the equation.

x^2 - 2x = 8

Take half of the coefficient of x and square it.

(-2/2)^2 = 1

Add the square to both sides of the equation.

x^2 - 2x + 1 = 8 + 1

Factor the perfect square trinomial.

(x - 1)^2 = 9

Take the square root of both sides of the equation.

x-1=
`√(9)`
x-1=±3

Isolate x to find the solutions.

Taking positive

x=3+1=4

x=4

Taking negative

x=-3+1

x=-2

The solutions are:

x = 4, -2

Answer 2

`x = -2,\;\;x=4`

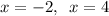
Explanation:

To solve the quadratic equation x² - 2x = 8 by factoring, subtract 8 from both sides of the equation so that it is in the form ax² + bx + c = 0:

`x^2-2x-8=8-8`

`x^2-2x-8=0`

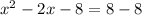
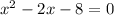
Find two numbers whose product is equal to the product of the coefficient of the x²-term and the constant term, and whose sum is equal to the coefficient of the x-term.

The two numbers whose product is -8 and sum is -2 are -4 and 2.

Rewrite the coefficient of the middle term as the sum of these two numbers:

`x^2-4x+2x-8=0`

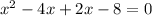
Factor the first two terms and the last two terms separately:

`x(x-4)+2(x-4)=0`

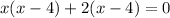
Factor out the common term (x - 4):

`(x+2)(x-4)=0`

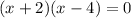
Apply the zero-product property:

`x+2=0 \implies x=-2`

`x-4=0 \implies x=4`

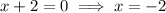
Therefore, the solutions to the given quadratic equation are:

`\boxed{x = -2,\;\;x=4}`