Question

Find the sizes of unknown angles

Answer 1

Explanation:

y and 20° are vertical opposite angles which means y is 20°.

z and 20° are on straight line which measure 180.

Therefore

z + 20° = 180°

z = 160°

x and z are vertical opposite therefore it is equal.

Therefore x = 160°

Answer: y = 20°

z = 160°

x = 160°

Answer 2

x = 160°

y = 20°

z = 160°

Explanation:

To solve this problem, we have to use a fundamental property of straight lines: vertically opposite angles are equal.

What are vertically opposite angles?

Vertically opposite angles are angles that are opposite each other and are formed when two straight lines intersect.

In this question, the vertically opposite angle pairs are x, z° and y, 20°.

Therefore, as vertically opposite angles are equal, we can say:

y = 20°,

x = z°

Next, we have to use the fact that angles around a point add up to 360° to find the sizes of angles x and z:

x + z + y + 20° = 360°

⇒ x + z + 20° + 20° = 360°

⇒ x + z + 40° = 360°

⇒ x + z = 360 - 40° [Subtracting 40° from both sides of the equation]

⇒ x + z = 320°

⇒ x + x = 320° [since x and z are equal to each other]

⇒ 2x = 320°

⇒ x =
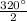`(320^(\circ))/(2)` [Dividing both sides of the equation by 2]

⇒ x = 160°

Therefore, z = 160°