Question

11. In a geometric sequence, t₂ = 24 and t5 = 81. Calculate S7, to the nearest hundredth.

Answer: 514.75

Answer 1

S₇ = 514.75

Explanation:

the nth term of a geometric sequence is

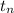`t_(n)` = a
`r^(n-1)`

where a is the first term and r the common ratio

given t₂ = 24 and t₅ = 81 , then

ar = 24 → (1)

a
`r^(4)` = 81 → (2)

divide (2) by (1) to eliminate a

`(ar^(4) )/(ar)` =
`(81)/(24)`

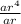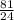
r³ =
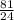`(81)/(24)` ( take cube root of both sides )

`\sqrt[3]{r^(3) }` =
`\sqrt[3]{(81)/(24) }`

r = 1.5

substitute r = 1.5 into (1) and solve for a

a × 1.5 = 24 ( divide both sides by 1.5 )

a = 16

the sum to n terms of a geometric sequence is

`S_(n)` =
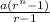`(a(r^(n)-1) )/(r-1)` , then

S₇ =
`(16((1.5)^(7)-1)) )/(1.5-1)`

=
`(16(17.0859375-1))/(1.5-1)`

=
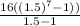
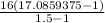
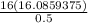`(16(16.0859375))/(0.5)` ( divide 16 by 0.5 )

= 32 × 16.0859375

= 514.75