Answer: 6sin( (pi/5)x ) + 1
==================================================
Step-by-step explanation:
I'll use the template
y = Asin(kx)+C
where,
- |A| = amplitude
- k = used to find the period
- C = midline
The highest and lowest we can go on the curve is y = 7 and y = -5 respectively. This is a distance of 7 - (-5) = 7 + 5 = 12 units. Half of this vertical distance is the amplitude, so we get 12/2 = 6 as the amplitude. This leads to either A = 6 or A = -6. I'll go with A = 6 for now.
One maximum point is at (-7.5, 7) and its adjacent neighbor max point is (2.5, 7)
This is a horizontal gap of 2.5 - (-7.5) = 2.5+7.5 = 10 units. This is the period of the sine curve because the graph repeats itself every 10 horizontal units along the x axis.
T = period = 10
k = 2pi/T
k = 2pi/10
k = pi/5
The last thing to determine is the value of C. To find this value, find the midpoint of the min and max.
C = (ymin + ymax)/2
C = (-5+7)/2
C = 2/2
C = 1
----------
To recap, we found these values
So we have
y = Asin(kx)+C
update to
y = 6sin( (pi/5)x ) + 1
which is the same as writing
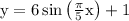
You can use a graphing tool such as Desmos or GeoGebra to confirm the answer is correct. Refer to the diagram below.