Question

3. Consider the acoustic plane wave p(t,rˉ)=Aej(ωt−kˉ⋅rˉ), where A,ω, and kˉ are known quantities. The wave propagates into a medium of known characteristic impedance Z0. Prove that the particle velocity corresponding to this wave has the following expression vˉ(t,rˉ)= p(t,rˉ)k^/ Z0a

Answer 1

The particle velocity corresponding to the given acoustic wave is $$\boxed{\vec v = \frac{A}{Z_0}\frac{\vec k}{k}e^{j(\omega t-\vec k.\vec r)}}$$where A,ω, and $\vec k$ are known quantities. The wave propagates into a medium of known characteristic impedance Z0.

Given, acoustic plane wave

`$$p(t,\vec r)=Ae^(j(\omega t-\vec k.\vec r))$$`

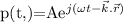
where A,ω, and
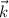`$\vec k$` are known quantities.

he wave propagates into a medium of known characteristic impedance Z0.Acoustic pressure,

`$$p(t,\vec r)=Ae^(j(\omega t-\vec k.\vec r))$$`

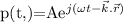
Particle velocity,

`$$\vec v=(1)/(j\omega\rho)\vec \\abla p$$`

`$$\vec v=(1)/(j\omega\rho)\begin{pmatrix} \hat i & \hat j & \hat k \\ (\partial)/(\partial x) & (\partial)/(\partial y) & (\partial)/(\partial z)\\ A e^(j(\omega t-\vec k.\vec r)) & A e^(j(\omega t-\vec k.\vec r)) & A e^(j(\omega t-\vec k.\vec r))\end{pmatrix}$$`

where
`$\rho$` is density of the medium and

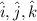`$\hat i,\hat j,\hat k$` are unit vectors in x,y and z direction respectively.

`$$=(A)/(j\omega\rho)\begin{pmatrix} \hat i & \hat j & \hat k \\ -k_x e^(j(\omega t-\vec k.\vec r)) & -k_y e^(j(\omega t-\vec k.\vec r)) & -k_z e^(j(\omega t-\vec k.\vec r))\end{pmatrix}$$`

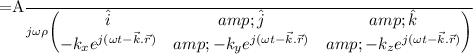
Substituting
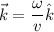`$\vec k=(\omega)/(v)\hat k$`where v is the velocity of the wave.

`$\vec k=(\omega)/(v)\hat k$`

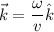
Substituting $Z_0 = \rho v$ and

`$$(1)/(Z_0) = (1)/(\rho v) = (j\omega)/(\rho) (1)/(j\omega v) = (j\omega)/(\rho) (1)/(k)$$`

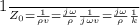
where k is the wave number,

$$\frac{\omega}{k} = v$$

Hence the particle velocity is,

$$\vec v = \frac{A}{j\omega \rho Z_0}\begin{pmatrix} \hat i & \hat j & \hat k \\ -\hat k_x & -\hat k_y & -\hat k_z\end{pmatrix}e^{j(\omega t-\vec k.\vec r)}$$

$$\vec v = \frac{A}{Z_0}\frac{\vec k}{k}e^{j(\omega t-\vec k.\vec r)}$$

Thus the particle velocity corresponding to the given acoustic wave is

$$\boxed{\vec v = \frac{A}{Z_0}\frac{\vec k}{k}e^{j(\omega t-\vec k.\vec r)}}$$

where A,ω, and $\vec k$ are known quantities. The wave propagates into a medium of known characteristic impedance Z0.