Question

Find rectangular coordinates of the polar coordinates (3,-2)

Find the polar coordinates of the rectangular coordinates (2, 5pi/4)

Answer 1

Explanation:

The equation of rectangular coordtion given polar coordinates are

`x = r \cos( \alpha )`

`y = r \sin( \alpha )`

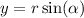
R is 2, and alpha is 5pi/4

So

`x = 2 \cos( (5\pi)/(4) ) = - √(2)`

`y = 2 \sin( (5\pi)/(4) ) = - √(2)`

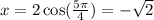
So our rectangular coordinates are

`( - √(2) , - √(2) )`

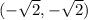
To convert from rectangular coordinates to polar coordinates

`r = \sqrt{ {x}^(2) + {y}^(2) }`

`\alpha = \tan {}^( - 1) ( (y)/(x) )`

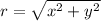
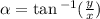
Since the point (3,-2), is in the fourth quadrant, our angle should be within (270 and 360 degrees)

`r = \sqrt{ {3}^(2) + ( - 2) {}^(2) } = √(13)`

`\alpha = \tan {}^( - 1) ( - (2)/(3) )`

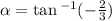
We about about

`\alpha = 326.31`

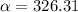
So our polar coordinates are

`( √(13) ,326.31)`

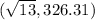
The second entry is in degrees. If you need to convert to radians, let me know