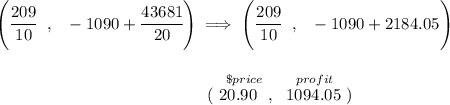well, profit equations are usually a parabolic path like a camel's hump, profit goes up up and reaches a maximum then back down, the issue is to settle at the maximum point, thus the maximum profit.
So for this equation, like any quadratic with a negative leading coefficient, the maximum will occur at its vertex, with x-price at y-profit.