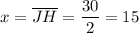Question

100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answer 1

Answer: x=15

Explanation:

If JH is a midsegment, then J is the midpoint of LK and H is the midpoint of KM. This also means that triangles JKH and triangles LKM are similar. Since H is the midpoint of KM, assume KM = 2y (KH=y). 30/x=2/1. Thus x=15.

Answer 2

x = 15

Explanation:

The midsegment of a triangle is a line segment that connects the midpoints of two sides of a triangle.

Therefore, if JH is the midsegment of ΔKLM then JH is parallel to LM, and triangles KJH and KLM are similar: ΔKJH ~ ΔKLM.

In similar triangles, corresponding sides are always in the same ratio.

Since JH is the midsegment of ΔKLM, then KJ is half the length of KL, and KH is half the length of KM. This means that JH is half the length of LM.

Given the measure of LM is 30:

`x=\overline{JH}=(30)/(2)=15`