Question

Find the value of the derivative for the given function.

Answer 1

`r'(1)=(1)/(16)`

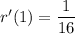
Explanation:

Find the derivative of the following function, then evaluate the function at a point.

`r=(1)/(√(5-\theta) ) ; \ r'(1)=??`

`\hrulefill`

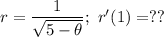
Taking the derivative of the function, r. Start by applying exponent rules.

`r=(1)/(√(5-\theta) )\\\\\\\Longrightarrow r=(1)/((5-\theta)^(1/2))\\\\\\\Longrightarrow r=(5-\theta)^(-1/2)`

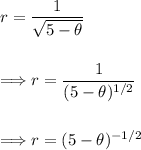
Now we can derive the function. Using the chain rule and power rule:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Chain Rule:}}\\\\(d)/(dx)\Big[f(g(x))\Big]=f'(g(x))\cdot g'(x) \end{array}\right}`

`\boxed{\left\begin{array}{ccc}\text{\underline{The Power Rule:}}\\\\(d)/(dx)\Big[x^n\Big]=nx^(n-1) \end{array}\right}`

`r=(5-\theta)^(-1/2)\\\\\\\Longrightarrow r'=-(1)/(2) (5-\theta)^(-1/2-1) \cdot -1\\\\\\\therefore \boxed{\boxed{r'=(1)/(2) (5-\theta)^(-3/2)}}`

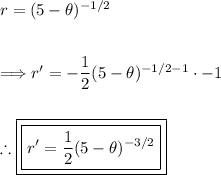
Thus, the derivative of the function is found.
`\hrulefill`

Now evaluating the function when θ=1.

`r'=(1)/(2) (5-\theta)^(-3/2)\\\\\\\Longrightarrow r'(1)=(1)/(2) (5-1)^(-3/2)\\\\\\\Longrightarrow r'(1)=(1)/(2) (4)^(-3/2)\\\\\\\Longrightarrow r'(1)=(1)/(2)\Big((1)/(8) \Big)\\\\\\\therefore \boxed{\boxed{r'(1)=(1)/(16) }}`

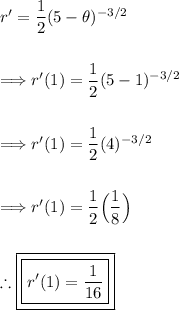
Thus, the problem is solved.