a) The percentage overspeed of the electric motor when the NIO EP9 autonomous track sports car reaches its top speed is given as follows:The maximum power output of the electric motor is 1342 bhp.
The full load speed of the electric motor is calculated as below:Full load speed,
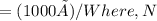 is the speed in rpm, P is the power in kWTherefore, the full load speed is given as:
is the speed in rpm, P is the power in kWTherefore, the full load speed is given as:
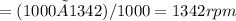 The top speed of the vehicle is 313 km/hr.
The top speed of the vehicle is 313 km/hr.
The overspeed of the motor can be calculated as follows:
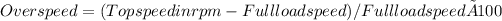 The acceleration of the vehicle from 0 to 100 km/hr is given as:Acceleration
The acceleration of the vehicle from 0 to 100 km/hr is given as:Acceleration
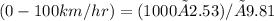 where, t is the time taken to accelerateThe acceleration of the vehicle from 0 to 200 km/hr is given as:Acceleration
where, t is the time taken to accelerateThe acceleration of the vehicle from 0 to 200 km/hr is given as:Acceleration
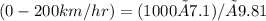 The acceleration of the vehicle from 0 to 300 km/hr is given as:Acceleration (0-300 km/hr) = (1000 × 15.9)/× 9.81c) The maximum tractive effort available and the tractive effort necessary to achieve each of the accelerations can be calculated as follows:The maximum tractive effort available can be calculated as:Tmax = × 9.81/rWhere, Pe is the maximum power output of the electric motor, r is the radius of the tyreTmax = (1342 × 1000)/ (2 × π × 0.35) × 9.81 = 4864 NThe tractive effort required to accelerate the vehicle from 0 to 100 km/hr can be calculated as follows:Te1 = 0.5 × Cd × ρ × A × (1)2/r + m × g × sin(θ)Te1 = 0.5 × 0.39 × 1.225 × 5.9 × (1000/3600)2/0.35 + 1700 × 9.81 × sin(0)Te1 = 6616 NThe tractive effort required to accelerate the vehicle from 0 to 200 km/hr can be calculated as follows:Te2 = 0.5 × Cd × ρ × A × (2)2/r + m × g × sin(θ)Te2 = 0.5 × 0.39 × 1.225 × 5.9 × (2000/3600)2/0.35 + 1700 × 9.81 × sin(0)Te2 = 11978 NThe tractive effort required to accelerate the vehicle from 0 to 300 km/hr can be calculated as follows:Te3 = 0.5 × Cd × ρ × A × (3)2/r + m × g × sin(θ)Te3 = 0.5 × 0.39 × 1.225 × 5.9 × (3000/3600)2/0.35 + 1700 × 9.81 × sin(0)Te3 = 18998 Nd) The drag force, downforce, and rolling resistance of the vehicle at different speeds can be calculated as follows:At 50 km/hr, the drag force of the vehicle is:FD = 0.5 × Cd × A × ρ × V2FD = 0.5 × 0.39 × 5.9 × 1.225 × (50/3.6)2 = 291 NThe downforce of the vehicle is given as:FDN = (CL × A × ρ × V2)/2FDN = (2.53 × 5.9 × 1.225 × (50/3.6)2)/2 = 550 NThe rolling resistance of the vehicle is given as:Fr = Cr × WFr = 0.01 × 1700 × 9.81 = 166 Ne) The power absorbed at top speed can be calculated as:Pe = (F × V)/ηWhere F is the total resistive force, V is the velocity, and η is the overall efficiency of the systemThe total resistive force can be calculated as:F = FD + FDN + FrThe overall efficiency of the system is given as 85%.The total resistive force at top speed is:F = 558 NThe power absorbed at top speed is:Pe = (558 × 313× 1000/3600)/0.85 = 576.17 kWThe current supply to each motor can be calculated as:I = Pe/VmWhere Pe is the power absorbed by the motor, and Vm is the voltage of the motorThe voltage of the motor is given as 800 V.The current supply to each motor is therefore:I = 576.17/800 = 0.72 ATherefore, the current supply to each motor is 0.72 A.
The acceleration of the vehicle from 0 to 300 km/hr is given as:Acceleration (0-300 km/hr) = (1000 × 15.9)/× 9.81c) The maximum tractive effort available and the tractive effort necessary to achieve each of the accelerations can be calculated as follows:The maximum tractive effort available can be calculated as:Tmax = × 9.81/rWhere, Pe is the maximum power output of the electric motor, r is the radius of the tyreTmax = (1342 × 1000)/ (2 × π × 0.35) × 9.81 = 4864 NThe tractive effort required to accelerate the vehicle from 0 to 100 km/hr can be calculated as follows:Te1 = 0.5 × Cd × ρ × A × (1)2/r + m × g × sin(θ)Te1 = 0.5 × 0.39 × 1.225 × 5.9 × (1000/3600)2/0.35 + 1700 × 9.81 × sin(0)Te1 = 6616 NThe tractive effort required to accelerate the vehicle from 0 to 200 km/hr can be calculated as follows:Te2 = 0.5 × Cd × ρ × A × (2)2/r + m × g × sin(θ)Te2 = 0.5 × 0.39 × 1.225 × 5.9 × (2000/3600)2/0.35 + 1700 × 9.81 × sin(0)Te2 = 11978 NThe tractive effort required to accelerate the vehicle from 0 to 300 km/hr can be calculated as follows:Te3 = 0.5 × Cd × ρ × A × (3)2/r + m × g × sin(θ)Te3 = 0.5 × 0.39 × 1.225 × 5.9 × (3000/3600)2/0.35 + 1700 × 9.81 × sin(0)Te3 = 18998 Nd) The drag force, downforce, and rolling resistance of the vehicle at different speeds can be calculated as follows:At 50 km/hr, the drag force of the vehicle is:FD = 0.5 × Cd × A × ρ × V2FD = 0.5 × 0.39 × 5.9 × 1.225 × (50/3.6)2 = 291 NThe downforce of the vehicle is given as:FDN = (CL × A × ρ × V2)/2FDN = (2.53 × 5.9 × 1.225 × (50/3.6)2)/2 = 550 NThe rolling resistance of the vehicle is given as:Fr = Cr × WFr = 0.01 × 1700 × 9.81 = 166 Ne) The power absorbed at top speed can be calculated as:Pe = (F × V)/ηWhere F is the total resistive force, V is the velocity, and η is the overall efficiency of the systemThe total resistive force can be calculated as:F = FD + FDN + FrThe overall efficiency of the system is given as 85%.The total resistive force at top speed is:F = 558 NThe power absorbed at top speed is:Pe = (558 × 313× 1000/3600)/0.85 = 576.17 kWThe current supply to each motor can be calculated as:I = Pe/VmWhere Pe is the power absorbed by the motor, and Vm is the voltage of the motorThe voltage of the motor is given as 800 V.The current supply to each motor is therefore:I = 576.17/800 = 0.72 ATherefore, the current supply to each motor is 0.72 A.