Question

Consider the following.

g(x) = 5 e^2.5x; h(x) = 5(2.5^x)
(a) Write the product function.
f(x) = ______
(b) Write the rate-of-change function.
f′(x) = ____

Answer 1

(a) The product function is

`f(x) =25e^((ln2.5+2.5)x)`

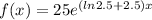
(b) The rate of change function is,

`f'(x) = 25e^((ln2.5+2.5)x)(ln2.5+2.5)\\`

(you can simplify this further if you want)

Explanation:

WE have g(x) = 5e^(2.5x)

h(x) = 5(2.5^x)

We have the product,

(a) (g(x))(h(x))

`(g(x))(h(x))\\=(5e^(2.5x))(5)(2.5^x)\\=25(2.5^x)(e^(2.5x))`

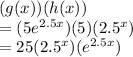
now, 2.5^x can be written as,

`2.5^x=e^(ln2.5^x)=e^(xln2.5)`

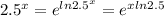
So,

`g(x)h(x) = 25(e^(xln2.5))(e^(2.5x))\\= 25 e^(xln2.5+2.5x)\\\\=25e^((ln2.5+2.5)x)`

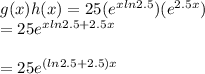
Which is the required product function f(x)

,

(b) the rate of change function,

Taking the derivative of f(x) we get,

`f'(x) = d/dx[25e^((ln2.5+2.5)x)]\\f'(x) = 25e^((ln2.5+2.5)x)(ln2.5+2.5)\\`

You can simplify it more, but this is in essence the answer.