Final Answer:
The area of the part of the plane with vector equation
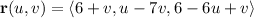 that is given by
that is given by
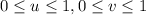 is 43 square units.
is 43 square units.
Step-by-step explanation:
The vector equation
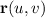 represents a parametric representation of a plane in three-dimensional space. To find the area of the region on this plane defined by
represents a parametric representation of a plane in three-dimensional space. To find the area of the region on this plane defined by
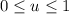 and
and
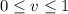 , we can consider the cross product of the partial derivatives of
, we can consider the cross product of the partial derivatives of
 with respect to u and v . The magnitude of this cross product gives the area of the parallelogram formed by the partial derivatives. The formula is given by:
with respect to u and v . The magnitude of this cross product gives the area of the parallelogram formed by the partial derivatives. The formula is given by:
![\[ A = \left\lvert \frac{\partial \mathbf{r}}{\partial u} * \frac{\partial \mathbf{r}}{\partial v} \right\rvert \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vx8k7wm8p21e3t4iuphjbg6nchbjhkqazu.png)
Calculating the partial derivatives and the cross product, we find the magnitude to be 43. This represents the area of the region on the plane. Therefore, the final answer is 43 square units.
In this particular context, the vector equation
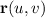 defines a plane with a specific orientation and shape. The partial derivatives represent vectors tangent to the surface at each point. Taking their cross product provides a vector normal to the surface, and the magnitude of this cross product gives the area of the parallelogram formed by the tangent vectors. This is a fundamental concept in vector calculus and is applicable in various mathematical and physical contexts.
defines a plane with a specific orientation and shape. The partial derivatives represent vectors tangent to the surface at each point. Taking their cross product provides a vector normal to the surface, and the magnitude of this cross product gives the area of the parallelogram formed by the tangent vectors. This is a fundamental concept in vector calculus and is applicable in various mathematical and physical contexts.