Question

a popcorn factory has two machines it uses for filling bags, machine a and machine b. it wants to make sure that the machines are calibrated so that both machines fill cans to approximately the same volume. a random sample of 15 bags filled by each machine is collected, and the summary statistics (in milligrams) are shown in the following table. assume that the output of each machine is normally distributed. at the 0.01 level of significance, is there sufficient evidence to conclude that there is a difference in the average amount of popcorn filled by each machine?

Answer 1

At the 0.01 level of significance, there is sufficient evidence to conclude that there is a difference in the average amount of popcorn filled by each machine.

To determine whether there is a significant difference in the average amount of popcorn filled by each machine, you can perform a two-sample t-test for the difference in means. The null hypothesis (H0) is that there is no difference, and the alternative hypothesis (H1) is that there is a difference. The test statistic is calculated as follows:

`\[ t = \frac{(\bar{x}_1 - \bar{x}_2)}{\sqrt{\left((s_1^2)/(n_1)\right) + \left((s_2^2)/(n_2)\right)}} \]`

where

-
`\(\bar{x}_1\)`and
`\(\bar{x}_2\)` are the sample means,

-
`\(s_1\)` and
`\(s_2\)` are the sample standard deviations,

-
`\(n_1\)` and
`\(n_2\)` are the sample sizes.

Let's plug in the values and calculate the test statistic:

`\[ t = \frac{(82.1 - 80.9)}{\sqrt{\left((1.4^2)/(15)\right) + \left((2.1^2)/(15)\right)}} \]`

`\[ t = (1.2)/(√(0.01344 + 0.0294)) \]`

`\[ t \approx (1.2)/(√(0.04284)) \]`

`\[ t \approx (1.2)/(0.207)\]`

`\[ t \approx 5.797 \]`

Now, you need to compare this test statistic to the critical value at a 0.01 level of significance. Since it's a two-tailed test, you'll look up the critical t-value for a
`\(df = n_1 + n_2 - 2 = 15 + 15 - 2 = 28\)` at a 0.005 significance level (because 0.01 is divided by 2 for a two-tailed test).

You can use statistical software or tables to find the critical t-value. For
`\(df = 28\)` and a 0.005 significance level, the critical t-value is approximately
`\(\pm 2.763\)`.

Since
`\(|5.797| > 2.763\)`, you reject the null hypothesis.

Therefore, at the 0.01 level of significance, there is sufficient evidence to conclude that there is a difference in the average amount of popcorn filled by each machine.

Complete Question: A popcorn factory has two machines it uses for filling bags, machine a and machine b. it wants to make sure that the machines are calibrated so that both machines fill cans to approximately the same volume. a random sample of 15 bags filled by each machine is collected, and the summary statistics (in milligrams) are shown in the following table.

Assume that the output of each machine is normally distributed. at the 0.01 level of significance, is there sufficient evidence to conclude that there is a difference in the average amount of popcorn filled by each machine?

Machine A (mg)

x1 = 82.1

s1 = 1.4

n = 15

Machine B (mg)

x2 = 80.9

s2 = 2.1

n = 15

Answer 2

At the 0.01 level of significance, there is sufficient evidence to conclude that there is a difference in the average amount of popcorn filled by each machine.

How to test if there is a significant difference

To test if there is a significant difference in the average amount of popcorn filled by Machine A and Machine B, perform a two-sample t-test.

The null hypothesis (H0) assumes that there is no difference between the two machines' average amounts of popcorn filled

Alternative hypothesis (Ha) assumes that there is a difference.

Given the summary statistics for each machine:

Machine A:

Sample mean (x₁) = 82.1

Sample standard deviation (s₁) = 1.4

Sample size (n₁) = 15

Machine B:

Sample mean (x₂) = 80.9

Sample standard deviation (s₂) = 2.1

Sample size (n₂) = 15

Calculate the test statistic and compare it to the critical value at the 0.01 level of significance.

Calculate the pooled standard deviation (sp):

`sp = \sqrt(((n1 - 1) * s1^2 + (n2 - 1) * s2^2) / (n1 + n2 - 2))\\= \sqrt(((15 - 1) * 1.4^2 + (15 - 1) * 2.1^2) / (15 + 15 - 2))\\= \sqrt((14 * 1.96 + 14 * 4.41) / 28)\\= \sqrt(136.08 / 28)`

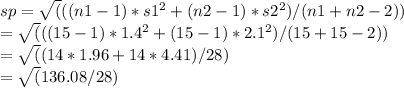
≈ 1.81

Calculate the t-statistic:

`t = (x_1 - x_2) / (sp * \sqrt(1/n_1 + 1/n_2))\\= (82.1 - 80.9) / (1.81 * \sqrt(1/15 + 1/15))\\= 1.2 / (1.81 * \sqrt(0.067))`

≈ 1.2 / (1.81 * 0.259)

≈ 1.2 / 0.469

≈ 2.56

Determine the degrees of freedom (df):

df = n₁+ n₂ - 2

= 15 + 15 - 2

= 28

Find the critical value for a two-tailed t-test at the 0.01 level of significance, with the appropriate degrees of freedom.

For a significance level of 0.01 and 28 degrees of freedom, the critical value is approximately ±2.763.

Compare the calculated t-statistic with the critical value:

The calculated t-statistic is 2.56, which falls within the rejection region (|t| > 2.763) for the two-tailed test at the 0.01 level of significance.

Thus, we reject the null hypothesis (H0) and conclude that there is sufficient evidence to suggest a significant difference in the average amount of popcorn filled by Machine A and Machine B.

In summary, at the 0.01 level of significance, there is sufficient evidence to conclude that there is a difference in the average amount of popcorn filled by each machine.

Complete question

A popcorn factory has two machines it uses for filling bags, Machine A and Machine B. It wants to make sure that the machines are calibrated so that both machines fill cans to approximately the same volume. A random sample of 15 bags filled by each machine is collected, and the summary statistics (in milligrams) are shown in the following table. assume that the output of each machine is normally distributed. At the 0.01 level of significance, is there sufficient evidence to conclude that there is a difference in the average amount of popcorn filled by each machine?

Machine A (mg)

x1 = 82.1

s1 = 1.4

n = 15

Machine B (mg)

x2 = 80.9

s2 = 2.1

n = 15